
RSA Encryption
Estimated Reading Time: 18 minutes
Introduction:
RSA (short for Rivest–Shamir–Adleman — named after its creators) is an asymmetric public-key encryption system that is very commonly used in real world applications. Despite its age (having been released in 1977), RSA encryption is still one of the most widely used asymmetric encryption algorithms in use today. Interestingly, it seems that an equivalent algorithm to RSA was created at GCHQ by James Ellis, Clifford Cocks, and Malcolm Williamson four years previously in 1973.
I learnt the theory behind RSA encryption primarily by choice as part of one of my freely chosen university projects, but I’m aware that it’s one of those things that many people seem to shy away from. In this post I am going to try to explain RSA Encryption in my own way, so I hope that it helps!
We’ll go over the theory in depth first, then look at implementing a simple RSA numeric key pair generator algorithm in both C++ and Python.
Theory:
Asymmetric Encryption:
Calling an encryption algorithm asymmetric is just a fancy way of saying that you need two different keys: one to encrypt, and one to decrypt. The public key is distributed to anyone who wants it, but the private key is kept only by the owner. The best example to explain this is that of “Alice and Bob”.
Alice and Bob:
To give it a real life analogy, say that Alice wants to send Bob a message in the mail, but she doesn’t want anyone else to be able to read it. By default she has nothing to lock it with, but what would happen if Bob had previously sent out unlocked boxes to every post office in the country? He keeps the keys to the boxes at home, but he distributes the boxes themselves around the country. Once a box is closed it cannot be unlocked without the key that Bob still keeps at home.
Alice goes to the post office and asks for one of Bob’s unlocked boxes. She then places her letter inside and closes the box. Now the only person who can open the box is Bob — not even Alice can reopen the box. The box is sent to Bob, who opens it with the private key he’s kept with him the entire time.
This is an example of asymmetric encryption. One method is used to encrypt the data (i.e. sealing it inside a locked box) and another method is used to decrypt the data (i.e. the owner of the box unlocking it with the key).
Symmetric Encryption:
As you might have guessed, symmetric encryption is where there is only one key in use. It might have to be encoded slightly differently for encryption or decryption, but it will be the same base nonetheless. With a symmetric encryption algorithm, Alice and Bob would have had to get together beforehand to share the key with each other.
A good example of this would be using a box with two keys to send the messages. Bob sends out the boxes (locked) to the post offices. Alice unlocks the box and enters her message, then relocks the box and sends it to Bob who can unlock it again and retrieve the message with his copy of the same key.
This works, but what if Alice and Bob can’t get together beforehand? How can Bob give one of the keys to Alice? If he posts it then it might get intercepted — he can’t use a locked box if she doesn’t have the key yet!
This is one of the fundamental problems with symmetric encryption. The initial exchange must be insecure in order to start sending secure messages, but if the unsecured key is intercepted then the entire conversation will be open!
Asymmetric vs Symmetric:
In summary:
| Asymmetric Encryption: | Symmetric Encryption: |
|---|---|
| Uses two keys: a public key for encryption and a private key for decryption | Uses one key to both encrypt and decrypt data. |
| Public key is distributed for anyone to use, private key must be kept a secret | The sole key must be kept hidden by both parties as it can be used to decode any communications if it’s intercepted |
| All communications are encrypted from the very beginning of the conversation — no “secret” exchange has to take place in order to securely send information. | Either the key must be sent insecurely across a network, or the people/computers involved must have a secret meeting to share the key before encrypted conversation can take place. |
| More difficult to use in three-way communication. | Can easily be used by many different people to send and read messages as a group. |
As a general rule, asymmetric encryption is a much safer bet to use over the internet.
Maths:
The RSA Encryption algorithm is based primarily around the concept of coprimality. For those who aren’t fans of maths, believe it or not, this isn’t nearly as complicated as you might think. A working knowledge of modular arithmetic is also really helpful.
I’m going to walk through the maths behind RSA Key generation with some example numbers, then I’ll provide a second example without breaking to explain the process.
Walk Through:
RSA Key generation starts with two prime numbers. These can be randomly selected or otherwise — they just have to be prime. In the real world these prime numbers would be absolutely huge, but for this post we’re just going to work with small primes. For a work-along example, let’s pick 11 and 13:
p = 11q = 13
We use these numbers to calculate two numbers which we’ll call n and phi. N is simply p and q multiplied together. Phi (usually represented with the Greek symbol φ ) is generally calculated with Euler’s Totient Function but I have an easier way to do it. Strictly speaking Phi is the number of integers that are coprime to n, which makes this the perfect time to talk about coprimality.
By definition, if two integers are coprime then they do not share a common divider, aside from the number one. In other words, the only integer that you could divide both numbers by (and still get a whole-number) is one. Take, for example, the numbers 8 and 15. We can factorise them like so:
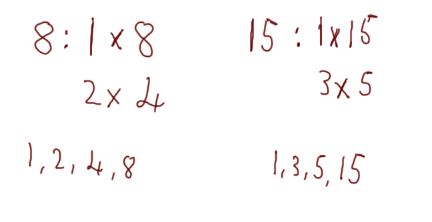
We can see that the factors of 8 are 1, 2, 4, 8 and the factors of 15 are 1, 3, 5, 15. The biggest number that is in both lists is 1, therefore the numbers 8 and 15 are coprime. Notice that any of the other factors from one number will not work for the other. For example, dividing 8 by 2 will give you a whole number, but dividing 15 by 2 will not. Equally, dividing 15 by 5 will give you a whole number, but dividing 8 by 5 will not. The only whole number that will divide both 8 and 15 to give a whole number is the number one.
As another example, take the numbers 25 and 32:
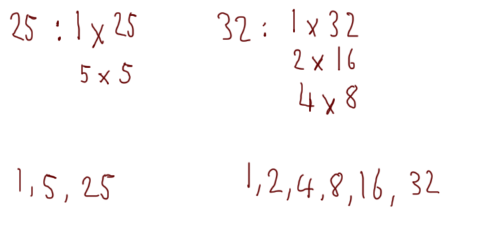
Once again, the greatest common divider (i.e. the biggest common factor between the two numbers) is 1, so the numbers are coprime.
One final example: take the numbers 8 and 12:
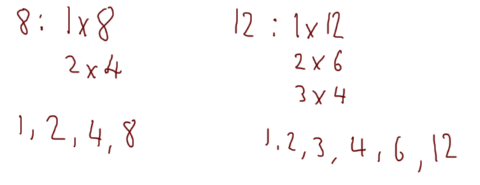
This time the greatest common divider is actually 4, so 8 and 12 are not coprime.
Assuming that all makes sense (if not, please feel free to leave a comment down below, or send me a message from Contact page), let’s get back to the RSA.
So, we know what n is (p*q) and we know that phi is the number of integers between 1 and n that are coprime to n. In other words, how many numbers between 1 and our calculated value of n are coprime to n.
In this case n = p*q = 11*13 = 143, so finding phi would mean finding the greatest common divider of every number from 1-143 and 143 itself, then taking a count of how many times the gcd is one. In other words, we’re looking for the number of integers between 1 and 143 that are coprime to 143. So we would do the process we used above with 1 and 143, then 2 and 143, then 3 and 143, all the way up to 142 and 143; the combinations that had a greatest common divider of one would be our coprime values, and phi would be the number of times this happened.
Fortunately, there’s an easier way (although understanding coprimality is still essential!).
We can calculate phi using: phi = (p-1) * (q-1).
So, for our example, phi = (11-1) * (13-1) = 10 * 12 = 120
Meaning that the information we know so far is:
p = 11q = 13n = 143phi = 120
Now that we know n and phi for our two prime numbers p and q, we can start calculating the encryption (public) and decryption (private) keys.
To find an encryption key e for our numbers (note that I said “an” — there will usually be more than one option!), we need to find a number that is less than phi, and coprime to both n and phi. In other words, the key should be greater than two and less than phi (2<e<phi); but it should also have a greatest common divider of 1 with both n and phi. The quickest way to find the potential encryption keys is with a program (much more on this later!):

e). If this makes sense to you now then great! Otherwise, we’ll be going over it in a lot more detail in the programming section.This program has returned the possible encryption keys. To make life easy, we’re just going to go with e = 7.
Our updated information looks like this:
p = 11q = 13n = 143phi = 120e = 7
The last thing we need to do here is find the private decryption key (d). Once again this is most easily done with a program to do the heavy lifting and is found with the equation d*e mod phi = 1 (or d*e % phi = 1). Interpretation: we’re multiplying d and e together, then dividing by phi. If the remainder is 1, then this is a valid value for d.
Once again we’re going to use a program to find numbers that satisfy the equation. We’ll go over this in a lot more detail later, but for now all that we need to know is that we’re looking for a number that’s just bigger than phi:

d). Note that the numbers we’re trying are from the number after phi, up to 1000 places after phi. You could go higher, but 1000 is enough for our purposes.Once again we’re just going to pick a key from the list of options. For the sake of simplicity we’ll say that d = 223.
We now have all the information we need in order to encrypt and decrypt data:
p = 11q = 13n = 143phi = 120e = 7d = 223
It’s important to note that the full keys are actually a combination of the key itself, and n. So, in our example, the final keys are:
- Public Key:
(7, 143) - Private Key:
(223, 143)
This is important because the equations we use to encrypt and decrypt data rely on knowing both parts of the key.
To encrypt data we take the ASCII codes of each character in a message and put it through this equation: character<sup>e</sup> mod n.
To reverse the process we use: character<sup>d</sup> mod n
If you’ve used the modulus operator when programming then that should make sense to you. Otherwise, here’s a brief introduction to modular arithmetic:
Cast your mind back to your first few years in school — back to when you were first learning about division. I’m guessing that the teacher taught you to use remainders? When you got up to a higher level you were told about decimal representation, but guess what — those remainders are about to come in handy!
Just as a very simple reminder, say we were asked to divide 75 by 60 — we could do it in our heads, or we could write it out like this:
We could also write this as 75 mod 60 = 15 (or 75 % 60 = 15 in many programming languages).
Now, let’s think about a clock.
A clock only goes up to 60 — after that it just loops back around to the start. What happens if you try to display 75 minutes on a clock? You get one whole hour, and fifteen remaining minutes. To put it another way, the number wraps around to the start when it reaches a certain point — in this case that point is 60. As another example:
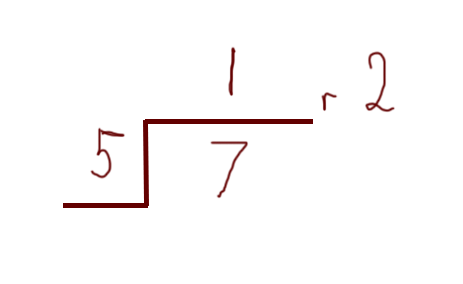
In the above example the “wrap-around” number is five. You could think of it as counting from 1 to 7. When you get to 5 you “store” the five you’ve already counted then start again at 1 for the remaining numbers. If the number were 11 then you would wrap-around twice (once at five, then again at 10), and have a remainder of 1.
This is the basis of modular arithmetic.
Right — now we can get back to those equations!
Let’s try this with a number first. Say we want to encrypt the number 24:
24<sup>7</sup> % 143 = 106
To get back we use the decryption formula:
106<sup>223</sup> % 143 = 24
Lets take a word example: “Hello”
In ASCII, “Hello” is 072 101 108 108 111
Applying the formula to the first code: 072<sup>7</sup> % 143 = 019
Using the encryption formula on each ASCII character code we get 019 062 004 004 045, which, when converted back into characters is, for the most part, not even printable.
To convert back we would put our numbers back into the decryption formula and once again get 072 101 108 108 111, or “Hello”.
Worked Example:
Let p = 17, q = 23
n = p*q = 391
phi = (p-1) * (q-1) = 16 * 22 = 352
So:
p = 17q = 23n = 391phi = 352
Calculating Encryption Key (e):

Let e = 57
Calculating Decryption Key (d):
Let d = 1161
Final Keys:
- Public Encryption Key:
(57, 391) - Private Decryption Key:
(1161, 391)
Example Usage:
15<sup>57</sup> % 391 = 304-
304<sup>1161</sup> % 391 = 15
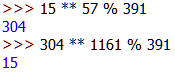
Summary:
- RSA Encryption relies on the generation of two different keys. These keys will be related to each other, but given one, you won’t be able to calculate the other.
- This is done by selecting two massive prime numbers and using them to calculate both the public key and the private key.
- In practical terms, numeric keys are usually generated, but are converted into string keys (like you would see if you generated keys with OpenPGP) before being used.
- The security of RSA relies on the fact that it’s incredibly difficult to factorise huge numbers down into the their prime products (like, unfeasible without quantum computers, kind of difficult).
- What this means is that, given a public key, you can’t then bruteforce the private key — not with today’s technology.
- Because of the fact that the private key never needs to be transferred, RSA encryption is widely used to authenticate many different methods of communication (including things like SSH and TLS).
Euclidean Algorithm:
The Euclidean Algorithm is considered a very efficient way of finding the greatest common divider of two numbers. We’re going to be programming a representation of it below, so it will be helpful to gain an understanding of how it works manually here first.
We already know that the greatest common divider of two numbers is the largest number that is a factor of them both. We saw the easy way of finding the GCD of two numbers in the coprimality section. This, unfortunately, is a lot less efficient when programmed into a computer, so instead we’re using the Euclidean Algorithm.
The basic format of the Euclidean Algorithm is this:
a = bk + rWhere:
- a and b are the numbers we’re working with
- k is a constant value
- r is the remainder
This will make a lot more sense with an example.
Say we’re trying to find the greatest common divisor of 24 and 16. We would begin to calculate it like this:
We would then repeat the process until the remainder is 0. a becomes the old b (i.e. 16) and b becomes the remainder (i.e. 8):
The remainder is 0, so the greatest common divider was 8, because 8 was the last value of b.
Let’s try one of the examples we used previously. We know that the numbers 8 and 12 have a common divider of 4 — we worked that out earlier, but let’s do it with the Euclidean Algorithm:
We’ll do one more example — this time with more than two steps. We’re going to use the numbers 105 and 75:
If we wanted, we could confirm this with our other method:
Great — we can now use the Euclidean Algorithm to find the GCD of any two numbers!
It might interest you to know that this algorithm can also be used to quickly convert between number bases — a very useful trick in computer science. That, however, is a lesson for another time.
Programming the Euclidean Algorithm:
We’ll be using the Euclidean Algorithm to calculate the GCD of lots of different values in the RSA program, so it’s a good idea to get to grips with it here. This is the algorithm programmed in Python:
def gcd(a, b):
if b == 0:
return a
return gcd(b, a%b)
This is best explained with an example. Let’s say that we’re trying to find the greatest common divider of 24 and 16. I’ve modified the function slightly to show this working at each stage:
Look familiar? It should! That’s one of the examples we did earlier. Notice that — just like we did when we were doing it manually — the program has calculated the answer in three stages. This is done through the use of nested function calls.
In the first iteration, the program has used the original values for a and b. It checks to see if b has reached 0 (it shouldn’t have because it hasn’t changed yet!), then it calls itself and sets b to be the new a and the remainder (i.e. a%b) to be the new b.
This recursion is a pain in the ass to get your head around, so don’t worry if you don’t fully understand it. What matters most is that you understand that this algorithm is an implementation of the Euclidean algorithm.
Programs:
The aim of this section is to demonstrate how to implement the RSA Encryption algorithm in C++ and Python 3.8. In real life you’re much more likely to use something like the OpenPGP key generator in Linux if you need to generate RSA Encryption keys, but I found that it was really beneficial to my understanding of the subject to know how to program the algorithm for myself. The programs will not be using values on as massive a scale as they would in the real world — purely so that you can test it out yourself to ensure that it’s working. In case you want to scale it up I’ll mention which lines of code to change when we get to them. These programs will also be very bare-bones: I’m only going to implement the actual key generation itself. Please feel free to expand them to your own uses.
Given that I’m literally programming the same thing in two languages, the following two sections are going to be pretty much identical. Pick the language you like the best and follow along!
C++:
I’m going to start with C++ because when I first wrote an RSA key value generator it was to upload into a Wemos ESP8266 board using the Arduino IDE. As such, I originally wrote the program in C++ so it makes sense to start with that.
As this is C++, the first thing we need to do is add our includes:
include <iostream> include <ctime> include <vector> using namespace std;
The next thing we’re going to need here is a function to find the GCD of two numbers. We already did this in Python during the Euclidean Algorithm section, but it’s going to be very slightly different in C++ — purely to deal with syntactical differences between the two languages:
int gcd(int a, int b){
if (b == 0){
return a;
}
return gcd(b, a%b);
}
(N.B: There is an inbuilt function in the standard library of C++ to find GCDs — we’re building one ourselves because it takes about three seconds and is beneficial to our understanding of the problem)
We next need to make a function that calculates prime numbers for us.
unsigned int prime_finder() {
unsigned int test_number = rand() % 100 + 10;
for (unsigned int i = 2; i < test_number; i++){
if (test_number % i == 0){
return prime_finder();
}
}
return test_number;
By definition a number is prime if it is only divisible by itself and one (i.e. there are no other numbers that will divide it and get a whole number as an output). The easiest way to check if a number is prime is to just test every number between 2 and the target — if the target it cleanly divided by the test number then the target cannot be prime. If we were to scale the numbers up to real-world levels then this could get really resource intensive, in which case we would have to use a more efficient method, but for now, this will do. If it finds a number that cleanly divides the target then the function calls itself, thus beginning the process all over again. Eventually the function will find a prime number, which will be returned to the main part of the program.
The second line of code in this block (the random number generation) is what you would need to change in order to get real-world values — but I warn you, the time for calculation will increase significantly!
We can now start programming our int main() function to perform the key generation for us.
We begin by seeding the random number generator with the current time. Without this, the randomiser in the prime finding function will not work correctly. Next we set two variables — p and q — to act as our initial prime numbers. Use our newly written prime_finder() to do so:
int main(){
srand(time(0));
unsigned long int p = prime_finder();
unsigned long int q = prime_finder();
We can then calculate n and phi:
unsigned long int n = p*q;
unsigned long int phi = (p-1)*(q-1)
Next we’re going to find ourselves a public key.
To do this we’re going to generate a bunch of valid keys, then pick one randomly from the list:
vector <int> pub_keys;
for (int i=2; i < phi; i++){
if (gcd(i,phi) == 1 && gcd(i,n) == 1){
pub_keys.push_back(i);
}
if (pub_keys.size() >= 100){
break;
}
}
unsigned int e = pub_keys[rand() % pub_keys.size()];
pub_keys.clear()
In this snippet we’re first declaring a vector of int elements: this is where we’ll store our possible keys. Next we loop through every number between two and phi, checking to see if it’s a possible public key; if it is, it gets added to the pub_keys vector. We then check to see if we have more than 100 potential keys — we don’t need that many! If we’ve already reached 100 possible keys the loop will then end; if we never actually reach 100, the loop will end naturally anyway. The next line selects a key at random and sets it to a variable e. Finally we clear the pub_keys list just as a matter of good practice.
Now that we have our public key, we can use it to calculate a private key. You’ll notice that the general format for this function is similar to the generation of the public key:
vector <unsigned int> priv_keys;
unsigned int i = phi + 1;
while (priv_keys.size() < 5){
if (i*e % phi == 1){
priv_keys.push_back(i);
}
i++;
}
unsigned int d = priv_keys[rand() % priv_keys.size()];
priv_keys.clear();
Once again we’re initialising an empty vector that will contain unsigned integers. We’re then using a while loop that will exit when the number of private keys found is at least five. These keys can get pretty big, relatively speaking, so we’re only going to look for five of them. Once again, we’re then going to add the keys to our vector. Outside of the loop, we’ll randomly select a key, then clear the vector.
The only thing we have left to do is neatly output the keys for the user to make use of:
cout << "Public Key: (" << e << "," << n << ")\n";
cout << "Private Key: (" << d << "," << n << ")\n";
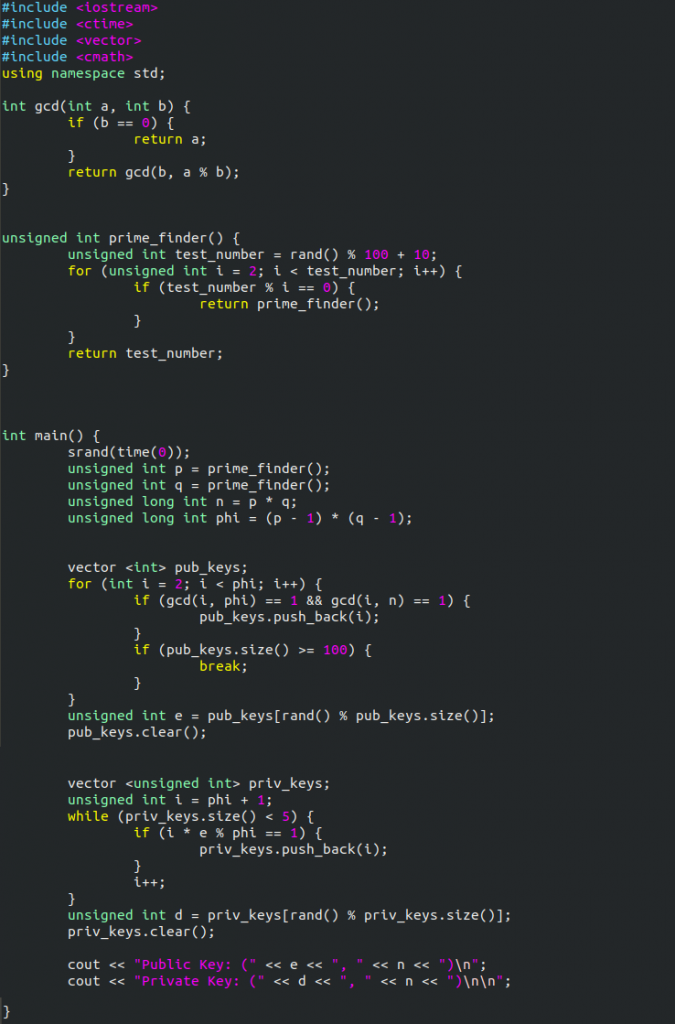
Here is a screenshot of the completed program:
Python:
Between Python and C++, I would definitely say that the Python implementation of this program is a lot easier to follow along with. That might, admittedly, be because Python is my “first language”, but hey — I’ll let you decide which is easier.
We’ll start by importing the sole library that we’re going to need:
import random
The first thing that we need to implement is a function to find the GCD of two numbers. In Python this is easy — we already defined such a function earlier:
def gcd(a, b):
if b == 0:
return a
return gcd(b, a%b)
Next we need to get ourselves a prime number generator. This is going to work by randomly choosing a number, then checking to see if it’s prime. If it is, the number will be returned, otherwise the function will call itself and the process will repeat.
def prime_finder():
test_number = random.randrange(10, 100)
for i in range(2, test_number):
if test_number % i == 0:
return prime_finder()
return test_number
Note that for the time being we’re just using prime numbers between 10 and 100. The second line in this code is the one that you would need to change in order to scale the numbers up. For the numbers that we’re using we’re Ok to just iterate through every number between two and the number we’re testing to check to see if it’s a prime number. If we were working with much bigger numbers a more efficient way of checking to see if a number is prime would need to be used, but this serves our purposes for now.
We can now start to calculate our initial numbers:
p = prime_finder() q = prime_finder() n = p*q phi = (p-1)*(q-1)
All pretty straight forward so far.
Next we’re going to calculate a list of possible encryption keys:
pub_keys = []
for i in range(2, phi):
if gcd(i, phi) == 1 and gcd(i, n) == 1:
pub_keys.append(i)
if len(pub_keys) >= 100:
break
e = random.choice(pub_keys)
del(pub_keys)
Here we’re intialising an empty list for the potential keys to go into. We’re looping through all numbers between two and phi checking them for suitability, and if they’re candidates to be the public key, we add them to the list. If the length of the list exceeds one hundred candidates and there are still more to check, we’re breaking out of it early. We don’t need that many options! Next we’re picking a key at random from the list, then, as a matter of form, we’re clearing the list — we don’t need it anymore.
Now that we have our public key, we can get on with calculating our private key. The process for this will be very similar to what we’ve just done, but the calculation itself is obviously different:
priv_keys = []
i = 2
while len(priv_keys) < 5:
if i * e % phi == 1:
priv_keys.append(i)
i += 1
d = random.choice(priv_keys)
del(priv_keys)
Here we’re once again initialising an empty list to contain our private keys. We’re then using a while loop to keep going until we have five candidates for our private key. These keys can get comparatively huge, so we’re limiting it to five. Then, once again we’re selecting a key at random from our list of possible candidates, and finally deleting the list.
The only thing left to do now is output the keys to our user:
print(f"Public Key: ({e}, {n})\nPrivate Key: ({d}, {n})")
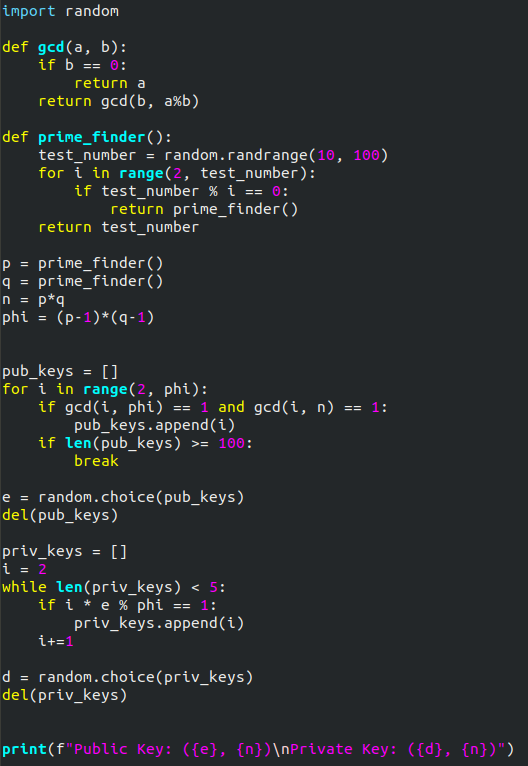
Here’s a screenshot of the completed program:
Final Thoughts:
RSA, despite its age, is still a very good concept to learn and understand — not least as an introduction to the concept of asymmetric encryption, which may serve you well when learning other algorithms. This is not necessarily an easy topic to get your head around, so well done if you’ve read through this post in its entirety! Hopefully the post has proven useful and you now have a slightly better understanding of the topic.
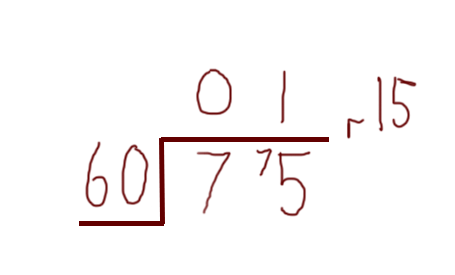

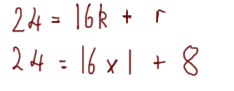
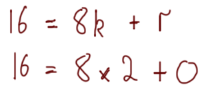
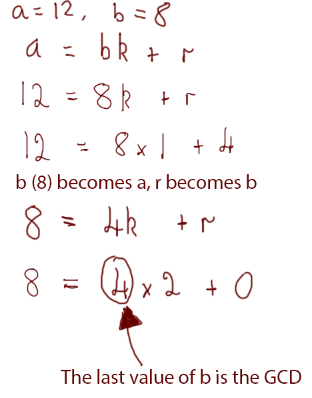

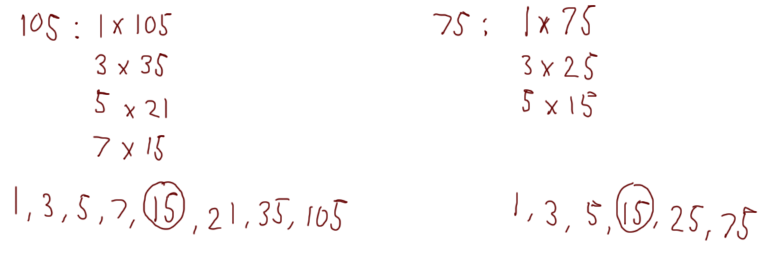

12 thoughts on “RSA Encryption”
Thank you!
Thank you very much for a very well and inspiring tutorial
Awesome blog!
Such an amazing and simple to understand blog. Thanks <3
Thank you so much! You explained it well enough that I could write a Powershell script without referencing your provided scripts.
I don’t have much to say other than THANK YOU ALOT…
it’s awesome 🙂
Thank you 🙂
Thanks for this greater job.
It’s appeared to be much simpler to fellow than what I thought.
Thank you, much easier in form of programing language!
Mindblowed. Thank you very much, i was looking for something exactly like this. Very very usefull. Thank you!
Thank you